Results are reported from a sample of 129 German-speaking individuals: patients diagnosed with schizophrenia and schizoaffective disorder (SSD, n = 42), major depressive disorder (MDD, n = 43), and healthy controls (HC, n = 44)31, which were age, sex and IQ-matched (Table 1). Speech samples were obtained through the task of describing four images of the Thematic Apperception Test (TAT)32. Word embeddings for each speech sample were obtained utilizing fastText and BERT. At the level of sentences, we employed the SentenceTranformers framework33, specifically using the ‘aari1995/German_Semantic_STS_V2’ model, which provides a 1024-dimensional vector for each sentence.
Preliminary analyses
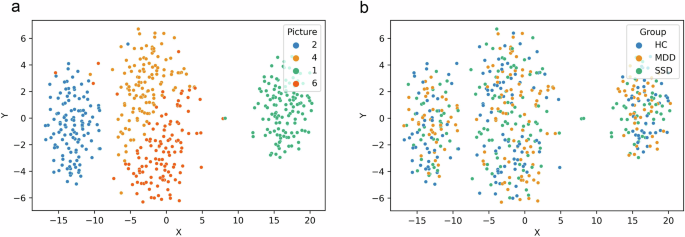
Our analytical pipeline is schematically presented in Fig. 1. In a preliminary and baseline semantic analysis, we calculated sentence embedding centroids for each text sample and investigated length effects on semantic similarity metrics. Centroids were calculated as in ref. 30, based on the average values for each dimension. After reducing 1024-dimensional embeddings into a 2-dimensional space with t-Distributed Stochastic Neighbor Embedding (t-SNE)34, a k-nearest neighbors (kNN) algorithm was used to classify pictures and groups. This algorithm showed near-ceiling performance for pictures, but chance performance for groups (Fig. 2): Accuracy=96.6%, precision (picture 1: 100%, picture 2: 98.4%, picture 4: 92.2%, picture 6: 95.7%), recall (picture 1: 99.2%, picture 2: 99.2%, picture 4: 96.7%, picture 6: 91.1%), average specificity=98.9%, and f1 score (picture 1: 99.6%, picture 2: 98.8%, picture 4: 94.4%, picture 6: 93.3%). Metrics for the performance of group classification were: Accuracy=64.9%, precision (MDD: 62.5%, HC: 64.3%, SSD: 70.6%), recall (MDD: 71.9%, HC: 77.6%, SSD: 44.7%), average specificity=82.4%, and f1 score (MDD: 66.9%, HC: 70.3%, SSD: 54.8%). These results indicate that while speech centroids based on sentence embeddings successfully distinguished between different pictures, thus capturing their inherent semantics, groups did not differ in terms of this baseline semantics. Put differently, when describing the same picture, different speech samples are rooted in the same semantic space and comparable for this reason. Figure 2 visualizes the centroids of each speech sample as reduced into a two-dimensional space.
Participants describe pictures, and their speech is transcribed and preprocessed. Sentences and words are analyzed separately. Sentence embeddings are generated using Sentence-Transformers and visualized using t-SNE to compute centroids and dispersion. Word embeddings are extracted using BERT and FastText to construct convex hulls and calculate their volume and area. Mean semantic similarity, maximum and minimum similarity, slope sign changes (SSC), crossings, and autocorrelation, are derived from embeddings. Euclidean distances between points in the semantic space are also calculated. These variables are used for classification and further analysis.
Sentence embeddings for each picture description were reduced to two dimensions using t-SNE, with centroids visualized for each speech. For the same speech centroids, in panel (a), colors indicate each picture description, and in panel (b), colors indicate group.
As a second preliminary step, we determined possible effects of speech quantity (word count and average sentence length) on semantic similarity assessments. Table S1 shows the total number of words for each participant and picture as well as average sentence lengths. In all pictures, mean length was higher in HC compared to both MDD and SDD (and higher in the MDD group compared to the SSD group). However, using t-tests Bonferroni-corrected for multiple comparisons to determine groups effects, only differences in mean sentence length in Pictures 2 and 4 (HC > SSD) remained statistically significant (corrected p-value: 0.0391 and 0.0278, respectively; see Figure S1). In addition, a negative correlation was observed between word count and mean semantic similarity when utilizing BERT (Pearson correlation, r = −0.57, p < 0.001), but not when using fastText (Pearson correlation, r = −0.001, p = 0.977). The same negative correlation was observed within each group when using BERT, and only in SSD when using fastText (Pearson correlation, r = −0.16, p < 0.05) (see Fig. S2). Figure 3 presents the correlation in a scatter graph for all groups with each point representing a single speech sample. Unlike with word count, there was no significant correlation between mean semantic similarity and average sentence length across all groups (using BERT, Pearson correlation, r = −0.05, p = 0.238; using fastText, Pearson correlation, r = −0.02, p = 0.511). These differences and their interaction with semantic similarity suggest speech quantity to be a possible confounding variable, which needs to be controlled when comparing groups for semantic similarity metrics.
In panel (a), using BERT model a negative correlation is depicted. In panel (b), no correlation was observed using fastText model.
Static and dynamic semantic analysis
Figure 4 summarizes group effects for semantic similarity variables, showing the standardized coefficients for the group variable and the p-values that were significant at the 0.05 level (additionally, an initial exploratory analysis comparing semantic similarity variables using a Kruskal-Wallis test is shown in Table S2). These results are derived from mixed-effects regression models for each dependent variable, which included both word count and average sentence length as predictors (see Eq. (1), Methods). In all regressions, Picture 1 and HC were used as baselines. Table S3 contains all the standardized coefficients and p-values, while detailed summaries for each regression can be found in Table S4. There were no significant group differences in mean semantic similarity, but there was a significant increase in maximum semantic similarity in SSD with respect to HC when using the BERT model. The remaining results clearly show a distinct pattern for MDD and SDD: in particular, significant differences were observed for MDD only when using fastText, while in SSD this was the case only for BERT. Specifically, MDD showed a lower mean crossing rate and higher autocorrelation, while SSD showed less sign slope changes (SSC). A trend in SSD was observed for a lower mean crossing rate (p = 0.087) and higher autocorrelation (p = 0.084) as well. Together, these dynamic metrics indicate that the time series of semantic similarities is more stable in the clinical groups. Additionally, the analysis revealed that the individual pictures had a significant effect on the semantic variables, as shown in Table S4. This highlights that in addition to speech quantity, picture effects need to be taken into account when computing semantic similarity related metrics, as was done here in all of our mixed effect models.
The plot displays standardized coefficients for the group variables, indicating group effects from separate regressions for each variable. Only significant coefficients are shown, with their corresponding p-values displayed next to the bars. Blue bars represent results for fastText, with light blue indicating MDD and blue indicating SSD. Green bars represent results for BERT, with light green for MDD and green for SSD.
Displacement and dispersion of semantic trajectories
We defined total displacement as the total length of a trajectory starting from a given location, measured as the cumulative Euclidean distances between word embeddings using the 300 dimensions of the fastText model. Table 2 shows larger displacement in SSD relative to HC, despite the unchanged centroids and mean semantic similarities as reported above (see Eq. (1), Methods). Unlike with semantic similarities, displacement exhibited no picture effect. The number of content words and average sentence length co-predicted displacement. To further explore the relationship between these predictors and the displacement variable, we ran the same regression with mean displacement (cumulative Euclidean distance divided by the number of content words) as the dependent variable. The results were also significant and in the same direction (see Table S5). There was no statistically significant difference in displacement across groups at the sentence level (see Table S6).
Next, the dispersion of a semantic space measures how spread-out sentence embeddings are relative to the centroid (average point). As seen in Table 3, MDD showed higher dispersion compared to HC in sentence embeddings with respect to the centroids of the speech samples (see Eq. (2), Methods). That is, although the centroids of the sentence embeddings thematically identified the different pictures and did not distinguish groups, as noted, sentences in MDD were more dispersed with respect to these centroids. Despite controlling for the number of sentences in the regression models, a negative effect of length was seen, with a greater number of sentences associating with lower dispersion.
Convex hulls
Finally, the convex hull of a given space of embeddings is a boundary capturing the extent and the outer limits of the distribution of embeddings, showing the furthest reaches of the sentence meanings in the semantic space. The boundary encloses all the embeddings in the tightest possible way, like a rubber band wrapped around them. With each sentence embedding serving as a vertex derived from the convex hull of all points, we calculated areas and hyper-volume (hereafter, ‘volume’) of the hyper-polyhedrons resulting, while varying the number of dimensions to gauge the sensitivity of this parameter (see Table S8 for this sensitivity analysis). Dimensionality reduction was necessary due to the requirement of having at least (n + 1) points (in this case, sentence embeddings) to construct a convex hull in n dimensions. Therefore, we mapped the original 1024 dimensions for each sentence embedding into a space of 5 dimensions, accounting for the number of sentences in each speech sample (mean = 19, SD = 8.2).
Our mixed-effect model (Eq. (3), Methods) considered the random effect of participants and the fixed effects of the group and the number of sentences produced. It revealed a significant decrease in the volume of the convex hull in SSD compared to HC (Table 4). When the analysis was repeated with the area of the convex hull as the dependent variable, SSD exhibited a smaller area as well, consistent with the volume decrease (p = 0.027) (see Table S7). Instead of regressing the volume directly, we first calculated the natural logarithm of the volume and then regressed this variable. This transformation stabilized the variance and normalized the distribution, allowing us to interpret the coefficients as percentage changes (see further Methods).
Table S8 shows the results of a sensitivity analysis using various numbers of dimensions (ranging from 3 to 9) to which the original 1024 dimensions were reduced. While the results remain largely consistent, it is important to note that increasing the number of dimensions will inevitably exclude an increasing number of speech samples with fewer sentences. Conversely, including speech samples with fewer sentences necessitates reducing the number of dimensions significantly, which leads to a loss of information.
Correlations to clinical scores
Significant correlations between the variables under analysis, which were averaged across pictures, and various symptoms scale scores are displayed in Fig. 5. Analogous correlational analyses for each picture separately can be found in Figure S3.
The heatmap illustrates the correlations between analyzed variables and clinical measures, including SAPS and SANS symptoms, the Hamilton Depression Scale (sum score), the Hamilton Anxiety Scale (sum score), the Young Mania Rating Scale, and the Global Assessment of Functioning. Colors range from blue (negative correlations) to red (positive correlations), with only significant coefficients displayed.
